HOME > カリクル就活 > 就活豆知識 > テストセンターの推論問題を対策して高得点を取ろう！例文も紹介

テストセンターの推論問題を対策して高得点を取ろう！例文も紹介

#テストセンター 推論

SPIの受検方式として、テストセンターで受験するケースは一定数あります。

そしてテストセンター受験をする就活生の中には、推論に関する設問に対して気になっている方も多くいるのではないでしょうか。

そこで本記事では、テストセンターの推論についてポイントを解説します。

例題も紹介するので、テストセンターの推論への準備にぜひお役立てくださいね。

テストセンターの推論とは

テストセンターとは、SPIの試験形式のうち指定された会場で受けるパターンのものです。

推論とは、SPIで出題される非言語問題の一分野であり、少ないデータから正答を導き出すことを求められます。

推論は、SPIの設問全体の中でも頻出の設問です。SPIの得点力アップを狙うなら、推論に対して十分な準備が求められると考えられます。

そしてテストセンター方式であっても頻出であることは同様であり、「いかに多くの設問を解けるか」にこだわって準備することが大切です。

テストセンターの推論問題を解くポイント5つ

ここでは、テストセンターの推論を解くためのポイントを以下の5点に整理して解説します。

1. 図や記号を書いて整理する
2. 問題文を正しく理解する
3. 設問内容から確実に言えることだけで判断する
4. 問題集を繰り返し解いて解き方を覚える
5. 重要な条件を見極める

ポイントを押さえることで得点力が上がることは多々あるので、ここで一緒にチェックしましょう。

①図や記号を書いて整理する

テストセンターの推論を解く際のポイントとしてまず挙げられるのが、図や記号を書いて整理することです。

頭だけで考えていると、どうしてもケアレスミスが多くなってしまうためです。図や記号を書くとなると、手間や時間がかかるように感じるかもしれません。

しかし図や記号をうまく活用することで、かえって正確かつスピーディーに解けるようになります。

本番で突然やろうとしてもうまくはできない可能性が高いことから、演習の段階から書いて整理する習慣をつけると良いでしょう。

②問題文を正しく理解する

SPIの推論にて得点力を上げるためには、問題文をしっかりと読んで正しく理解することも大切です。

設問文の中にある重要な前提を読み間違えないように、気を付けて読み進める必要があります。

「しっかり読む」と言われると当たり前のことのように聞こえるかもしれませんが、本番で緊張すると読み飛ばしや誤読が発生しやすくなるものです。

情報の漏れや勘違いを防ぐために、正確に設問を読むことを普段から意識するようにしましょう。

③設問内容から確実に言えることだけで判断する

推論もんだしでは、設問内容から「確実に言えること」だけで判断する姿勢も大切です。

設問に前提として書かれていないことを勝手に推測して選ぶと、多くの場合誤答につながります。

先ほどお話しした通り設問を正しく読み、前提を勘違いしないように気をつけることも大切でしょう。

設問を読んで整理しても正答が分からないようであれば、設問の前提を誤って理解している・読み落としている可能性を疑うことが大切です。

④問題集を繰り返し解いて解き方を覚える

推論の得点力を高めるには、問題集を繰り返し解いて基本的な解法を覚えることが重要です。

SPIの推論では、似たようなパターンで解ける設問が多いと言えます。そのため、解き方を覚えることで解くスピードが自然に上がります。

新しい設問でもいずれかのパターンに当てはめて対応できることが多くあることから、得点力が高まるだけでなく安定しやすくもなるでしょう。

パターンは短期間で無理に暗記しようとすると大変なので、1冊の問題集を繰り返し何度も解く中で自然に覚えていくことをおすすめします。

⑤重要な条件を見極める

テストセンターの推論の設問では、重要な条件を見極めることが重要です。限られた時間でスムーズに正答するには選択肢を消去法で少なくすることが求められます。

設問を読んでポイントに早く気づければ、対応にかかる時間を短縮して正答率も高めることが可能です。

重要なポイントの見極めには一定の練習が必要なので、繰り返し問題集を読んでポイントをつかむ訓練をするようにしましょう。

繰り返し設問を解いていく中で、重要なポイントに対する勘が培われていきます。

テストセンターの推論の問題例5つ

ここでは、テストセンターの推論に関して、設問例を以下のパターン別に5つ紹介します。

1. 順序
2. 密度
3. 発言の正誤
4. 平均
5. 位置関係

①順序

＜例題＞ Q、W、E、R、Tの5人がテニスの総当たり戦をした。 順位に関しては、以下のことが言える。なお、同じ順位のチームはない。 1.TはRよりも1つ順位が上 2.Qは一位ではない 3.EはWよりも順位が下 次の推論の内、必ずしも誤りと言えないものはどれか。 丙：Wは2位だった 乙：Qは3位だった 丙：Eはビリだった （選択肢） A：甲だけ B：乙だけ C：丙だけ D：甲と乙の両方 E：甲と丙の両方 F：乙と丙の両方 G：甲と乙と丙の全て H：全て間違い （正答）F：乙と丙の両方

順序の設問では、設問から得られる前提より考えられる順位を書き出していくことが重要です。

たとえば1.の選択肢より、TとRは連続した順位であることが分かります。書き出した前提を元に、選択肢を1つずつ検証していきましょう。

②密度

＜例題＞ 以下は、Q市、W市、E市の３つの市の人口密度を示している。 Q市：320人/㎢ W市：400人/㎢ E市：240人/㎢ E市の面積はW市の2倍であり、Q市の面積はW市の面積と同じである。 この時、次のアとイの推論について正しいものを選べ。 甲：E市の人口はW市よりも多い 乙：E市とQ市が合併したら、E市の人口密度と同じになる （選択肢） A：甲も乙も正しい B：甲は正が乙はどちらともいえない C：甲は正しいが乙は誤り D：甲は定かではないが、乙は正しい E：甲は定かではないが、乙は誤り F：甲も乙も定かではない G：甲は誤りだが、乙は定かではない H：甲は誤りだが、乙は正しい I：甲も乙も誤り （正答）C：甲は正しいが乙は誤り

密度の設問では、「面積×人口密度=人口」の指揮に設問の内容を当てはめて考えます。

上記のように面積の具体的な数値が分からない場合、設問の前提から「Q=①、W=①、E=②」などと適当な数字に置き換えて計算すると良いでしょう。

③発言の正誤

コインを9回だけ回して、表と裏が出た数をそれぞれカウントした。そして最終的に、以下の事実がわかった。 1.表が出た回数は7回である 2.裏が出た回数のほうが少ない 3.表が出た回数は奇数である 上記の記述は必ずしもすべて正しいとは言えない。 以下の発言のうち、正しいのはどれか。 甲.1が正しいなら、2も必ず正しい イ.2が正しいなら、3も必ず正しい ウ.3が正しいなら、1も必ず正しい （選択肢） A：甲だけ B：乙だけ C：丙だけ D：甲と乙の両方 E：甲と丙の両方 F：乙と丙の両方 G：甲と乙と丙の全て H：全て間違い （正答）A

発言の正誤を判断する設問は、情報を整理して1つずつ当てはまるかどうかを判断していきます。

難しく見えて整理すると簡単なことも多いので、焦らずに設問からわかることのみを整理して臨んでみましょう。

④平均

＜例題＞ Q、W、E、Rの4人がテスト（100点満点）を受けたところ、以下の通りの結果になった。 Ⅰ　4人の平均点は70点だった Ⅱ　QとWの平均点は60点だった Ⅲ　EはRよりも20点高かった 上記の事実より、必ず正しいと考えられるのどれか。 ア.WはRよりも高得点である イ.QかWのどちらかは60点以下 ウ.QはWよりも高得点である （選択肢） A：甲だけ B：乙だけ C：丙だけ D：甲と乙の両方 E：甲と丙の両方 F：乙と丙の両方 G：甲と乙と丙の全て H：全て間違い （正答）B：乙だけ

平均の設問では、設問からそれぞれの点数に関して分かる範囲で特定・推測していきます。必ずしも全員の正確な点数が分かる訳ではない点に注意です。

上記の設問では、QとWの点数は平均しかないため正確には分かりませんが、平均が60点なのでどちらかが必ず60点以下になると言えるでしょう。

⑤位置関係

＜例題＞ Q、W、E、Rの4人が以下のような2階建てのアパートに住んでいる。 1人が1部屋に住むとして、次のことが分かっている。 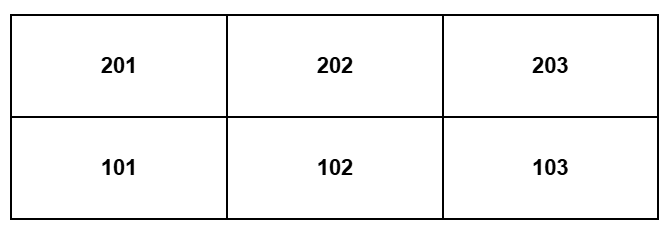1.102と103には住んでいる人がいない 2.Qの部屋の下にはEが住んでいる このとき、Wが住んでいる部屋として可能性があるのは何番か。 ＜選択肢＞ A. 201もしくは101 B. 202もしくは203 C. 103もしくは201 D. 202もしくは102 （正答）A.201もしくは101

位置関係の設問の場合、設問の前提から確定していると言えることだけまず整理すると、正答率が高まります。

消去法でまず明らかに誤りと言える選択肢を消し、残りの選択肢を1つずつ検証してみると良いでしょう。

テストセンターの推論問題を対策して高得点を取ろう

テストセンターの推論に関する設問は、SPI全体においても出題頻度が最も高い分野です。

推論への準備を行うことでSPIの得点力アップが期待できることから、本記事もぜひご参考にして高得点を目指してくださいね。