HOME > カリクル就活 > SPI推論の問題例をパターン別に紹介｜解くコツや対策方法も解説

SPI推論の問題例をパターン別に紹介｜解くコツや対策方法も解説

SPI推論問題例SPI推論就活SPI推論SPI推論対策

就活の適性検査対策を行うのであれば、SPI対策は欠かせないものでしょう。

そしてSPI対策には、「SPI推論」の得点力アップが重要です。しかしSPI推論に対して、対策方法に不安を覚えている方もいるのではないでしょうか。

本記事では、SPI推論の概要や対策方法、解答の秘けつなどを詳しく解説します。

問題例も紹介しているので、ぜひ対策にお役立てくださいね。

SPI推論とは

SPI推論とは、与えられた情報から正しい選択肢を選ぶ形式の問題です。

問題自体は比較的シンプルですが、論理的思考能力の違いによって得点差が出ると考えられます。

また、1つの問題にかけられる時間が1分程度であることを考えると、基本的な計算処理をスムーズに行う能力も必要だと言えるでしょう。

各問題に余計な時間を使わないためにも、問題演習を繰り返して出題傾向や解答の流れを把握することが重要です。

SPI推論を対策すべき2つの理由

SPI推論はしっかりとした対策が必要な問題であると考えられます。SPI推論の対策が必要な理由は、主に以下の2点です。

1. 最頻出である
2. 慣れが必要

①最頻出である

SPI推論の対策が必要な理由としてはまず、計数問題の中でも出題頻度が最も高い問題である点が挙げられます。

頻出の問題であることから、ここでうまく得点できないと全体の得点力が大きく落ちてしまうでしょう。

一方でSPI推論に対して十分に対策して解答できるようになれば、全体での高得点も期待できます。

最頻出であるだけに他の就活生も一定の対策をしてきていると考えて、できる限り対策を取ることがおすすめです。

②慣れが必要

スムーズな解答には一定の慣れが必要であることも、SPI推論の対策をすべき理由の1つだと言えます。

SPI推論の解答には明確な公式が存在しているわけではなく、慣れていないと難しさを感じやすいと考えられるのです。

一方でもんだい演習を繰り返してえパターンに慣れてしまえば、時間をかけずスムーズに解くことも十分にできます。

「対策をして十分な演習をすれば得点できるようになる」と考えて、前向きに勉強する分野だと考えられるでしょう。

SPI推論を解く3つのコツ

ここでは、SPI推論を解く際の戦略として以下の3点を紹介します。

1. 情報を図式化する
2. 文章をよく読む
3. 全ての事象を書き出す

①情報を図式化する

SPI推論を解く際の秘けつとしてまず挙げられるのが、問題文から得られる情報の図式化です。

問題文の情報を頭の中だけで考えようとすると、複雑で分かりにくく感じる可能性があります。また頭の中のみで考えるとケアレスミスをしてしまう可能性が高まりますよ。

記号や図を活用することで情報を整理しやすくなり、ケアレスミスが減る効果も期待できるでしょう。

図式化に決まりはありませんが練習していないと難しいので、自分が図式化しやすいやり方を練習しておくことが重要ですよ。

②文章をよく読む

文章をよく読んで解答する姿勢も、SPI推論に回答するためには重要だと言えます。

SPI推論の問題文には独特の言い回しもあり、集中して読まないと認識を誤ってしまう恐れがあるためです。

問題文の内容を誤って認識したままでは、正しい選択肢を選ぶことはできません。

分かりにくい表現があれば自分が理解しやすい表現に置き換えて、問題文の情報からから確実に言えることだけで判断するようにしましょう。

③全ての事象を書き出す

SPI推論の解答にあたっては、すべての事象を書き出すことも重要です。問題によっては、頭の中のみで整理するのが困難なこともあります。

焦って頭の中だけで急いでやろうとすると、普段は起きないようなミスが発生してしまうものです。

冷静にすべての事象を書き出す方法の方がかえってスムーズに解答でき、ケアレスミスも発生しにくいいためおすすめでしょう。

ただしやはり本番でいきなりやろうとするとスムーズにできないことから、繰り返し練習して慣れておくことが大切です。

SPI推論の対策方法

SPI推論の対策を進めるうえでは、問題集を繰り返し解く方法が最も確実でおすすめです。

問題集を繰り返し解くことで問題のパターンが自然と身に着きやすく、理解できなかった問題も繰り返し解くことで理解できるようになります。

問題集は何冊も手に入れてあれこれと手を付けるのではなく、まずは1冊の問題集に繰り返し取り組むことが重要でしょう。

問題を覚えてしまうくらいまで繰り返し取り組むことで、問題から解法パターンをスムーズに想起しやすくなります。

【解説つき】SPI推論の例題6つ

ここでは、SPI推論の例題を以下の6つに分けて紹介します。

1. 例題1：順序（順位や順番、並び方に関する問題）の問題
2. 例題2：対戦の問題
3. 例題3：正誤判定の問題
4. 例題4：割合の問題
5. 例題5：整数の問題
6. 例題6：位置関係の問題

例題1

<例題> A、B、C、D、Eの5つのチームで毎年行われている野球大会を実施した。去年と今年の順位について、次のことがわかっている。ただし、同率同位のチームはない。 1.Aは今年の大会で、昨年から順位を3つ下げた。 2.昨年も今年もDはEの1つ下の順位だった。 3.Bの今年の順位は2位だった。 左から順に1位〜5位のチームを並べたところ、今年の順位として正しいものを以下のアからエの中で1つ選べ。 ア.EBDCA イ.EBDAC ウ.CBEDA エ.CBEAD 正答：ウ

上記は、「順序（順位や順番、並び方に関する問題）」の問題と呼ばれています。

与えられた情報を簡単なメモにして整理し、考えられる順序を部分的にも良いので1つずつ書き出しましょう。

書き出した順序から消去法で選択肢を絞り、残りのパターンを書き出して正しいか考えると、正答率が高まります。

例題2

<例題> A、B、C、Dの４チームが、サッカーのリーグ戦を行った。その試合結果について、以下のことが分かっている。 1.Aは1勝2敗だった 2.AはBに勝った 3.CはAに勝った 4.DはBに勝った 5.引き分けの試合は無かった 次の推論のうち、必ずしも誤りとはいえない推論はどれか。 ア.Aは1勝2敗だった イ.Cは全勝だった ウ.Dは1勝2敗だった A：アのみ B：イのみ C：ウのみ D：アとイの両方 E：アとウの両方 F：イとウの両方 G：アとイとウすべて H：なし 正答：D

上記は、「対戦の問題」と呼ばれる問題です。多くの情報が細かく出てくることから、頭だけで考えず書き出すことが重要だと言えます。

多くの場合、表に書き出してまとめると、間違えが少なくスムーズに応えることが可能でしょう。

例題3

<例題> A、B、Cが同じ映画を鑑賞したうえで、次のように発言した。 A：この映画には日本人が出てきた。 B：この映画には少なくとも日本人かアメリカ人が描かれている。 C：この映画にはアメリカ人が出てきた 全員が本当のことを言っているとは限らない。 そこで、以下の推論のうち正しいものを一つ選びなさい。 ア：Bが正しければAは必ず正しい イ：Cが正しければBは必ず正しい ウ：Aが正しければCは必ず正しい 正答：イ

上記は、「正誤判定の問題」と呼ばれる問題です。多くの場合、複数人の発言を確認して矛盾を見つけ出すことが求められます。

各登場人物の発言からどこまでのことが言えるのか、整理しながら考えられるかどうかが重要でしょう。

例題4

<例題> ある店舗の売上について調査したところ、毎月売り上げが15%ずつ増えていることが分かった。この時、次の推論について述べたものとして、AからCの中で正しいものを1つ選べ。 「この店舗の売上は、この2ヶ月間で30%増加した」 ＜選択肢＞ ア：正しい イ：どちらともいえない ウ：誤り 正答：ウ

上記は、「割合の問題」と呼ばれる問題です。人口密度や食塩水の濃度、そして上記の問題のように売上の問題などが出題されます。

基本的には簡単な算数の計算によって回答を導き出せますが、ちょっとした見落としや勘違いには気負を付けなくてはいけません。

たとえば上記の問題の場合、「2か月分だから15％+15％で30％」とすぐに結論を出すと誤答になってしまいます。

最初の状態を100とすると1ヵ月目は「100×1.15=115」で15％増加です。しかし二か月目は「115×1.15=132.25」となり、最初の状態から32.25％増が正解です。

例題5

<例題> A、B、Cのボールを合計16個買った。ただし、どのボールも1個以上は買った。それぞれの買った数について、以下のことが分かっている。 1.AとBのボールは同じ個数である。 2.CのボールはAのボールの2倍である。 このとき、Ｃが持っているボールの個数は何個か。 正答：8個

上記は、「整数の問題」と呼ばれています。文章から方程式を作り、解答することが基本となっている問題です。

上記は「A=x」と置き換えて、ボールの総数から方程式を組み立てて解答します。

基本的には中学レベルの数学で対応できると思われますが、以下に焦らずスピーディーに対処できるのかがカギです。

例題6

<例題> 以下のように円形に並んだ4つの席のいずれかに、A・B・Cの3人が座っている。 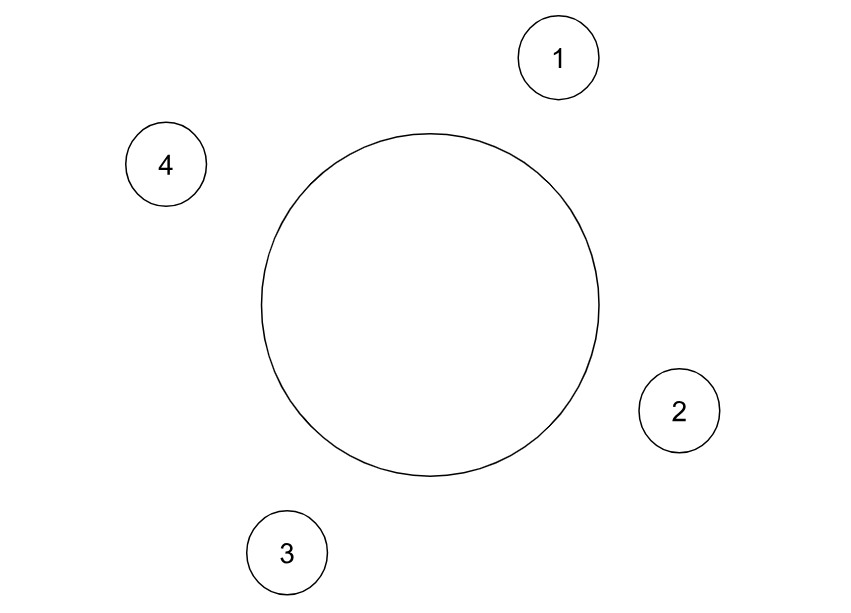各自の座り方については、以下のことが分かった。 1.BとCは隣り合って座っていた。 2.4番の席には、誰も座っていなかった。 この時、Aが座っていた可能性のある席の番号はいくつか。 ア：1 イ：2 ウ：3 エ：1か2 オ：1か3 カ：2か3 正答：オ

上記は、「位置関係の問題」と呼ばれています。簡単なイメージ図と条件が与えられて、正しい位置関係を推測することが基本です。

それぞれの情報から言えることをメモして、可能性を整理していくと正答にたどり着きやすいでしょう。

上記の場合は4には誰も座れないので、BとCは①「1・2」か②「2・3」の2つの組み合わせのいずれかでしかありえません。

そのためAは、①の場合「3」、②の場合「1」に座ることになります。

SPI推論の対策をして高得点をとろう

SPI推論はSPIの中でも出題頻度が最も高く、しっかりと対策をしておかないと全体の得点に影響を及ぼす可能性があります。

一方で対策を取ることで高得点も十分に狙える分野でもあるため、本記事をぜひともご活用いただきSPI攻略にお役立てくださいね。